Řešené příklady

Vypočítejte molární hmotnost kyseliny chlorečné.
Řešení
| $$M({\rm##sHClO_3})=?$$ |
Budeme postupovat stejně jako v případě výpočtu relativní molekulové hmotnosti $$M{\rm_r}$$ pro kyselinu chlorečnou. Z tabulky zjistíme jednotlivé atomové relativní hmotnosti všech prvků v molekule kyseliny. Protože molární hmotnost ($$M$$) je číselně rovna relativní molekulové hmotnosti ($$M{\rm_r}$$), provedeme následující výpočet.
Výpočet
$$M({\rm##sHClO_3})=##sA{\rm##s_r}({\rm##sH})##s+##sA{\rm##s_r}({\rm##sCl})##s+3\cdot##sA{\rm##s_r}({\rm##sO})=##s1{,}008##s+35{,}45##s+##s3\cdot##s15{,}999##s\doteq##s84{,}455\,##s\rm##s\frac{g}{mol}$$
Odpověď
Molární hmotnost kyseliny chlorečné je $$84{,}455\,##s\rm##s\frac{g}{mol}$$.

Jaká je hmotnost jednoho molu atomů vodíku?
Řešení
| $$n({\rm##sH})=1\,\text{mol}$$ |
| $$m({\rm##sH})=?$$ |
Nejprve v tabulce vyhledáme molární hmotnost vodíku.
$$M({\rm##sH})=1{,}008\,##s\rm\frac{g}{mol}$$.
I. způsob
Jednoduchou úvahou (a ze znalosti definice molární hmotnosti) hned vidíme, že molární hmotnost udává hmotnost jednoho molu.
Odpověď
Jeden mol atomů vodíku váží $$1{,}008\,\rm##sg$$.
II. způsob
Příklad můžeme vyřešit i pomocí dosazení známých hodnot látkového množství a molární hmotnosti do vzorce.
§§m({\rm##sH})=n({\rm##sH})##s\cdot##sM({\rm##sH})§§
Výpočet
$$m({\rm##sH})=n({\rm##sH})##s\cdot##sM({\rm##sH})=1##s\cdot##s1{,}008\doteq##s1{,}01\,\rm##sg$$
Odpověď
Jeden mol atomů vodíku váží přibližně $$1{,}01\,\rm##sg$$.

Podle nutričních tabulek jsou doporučené denní dávky draslíku, elementárního železa a soli následující:
| Prvek | Doporučená denní dávka |
| $$\rm##sFe$$ | $$15\,\rm##smg$$ |
| $$\rm##sK$$ | $$370\,\rm##smg$$ |
| $$\rm##sNaCl$$ | $$5\,\rm##sg$$ |
Určete doporučenou denní dávku vybraných látek v molech.
Řešení
| $$m({\rm##sFe})##s=##s15\,\rm##smg##s=0{,}015\,g$$ |
| $$m({\rm##sK})##s=##s370\,\rm##smg##s=0{,}37\,g$$ |
| $$m(\rm##sNaCl)##s=##s5\,g$$ |
Ke zjištění látkových množství jednotlivých doplňků potravy potřebujeme nejprve znát jejich molární hmotnost $$M$$.
| $$M({\rm##sFe})=55{,}845##s\frac{\rm##sg}{\rm##smol}$$ |
| $$M({\rm##sK})=39{,}098##s\frac{\rm##sg}{\rm##smol}$$ |
| $$M({\rm##sNaCl})=58{,}44##s\frac{\rm##sg}{\rm##smol}$$ |
Začneme nejprve solí. Pokud víme, že 1 mol soli váží $$58{,}44$$ gramů a náš denní příjem činí $$5$$ gramů (což je trochu méně než desetina hmotnosti jednoho molu), můžeme očekávat, že toto množství bude také téměř desetina molu. K přesnému výpočtu použijeme vzorec
$$n=\frac{m}{M}$$.
Výpočet
§§n({\rm##sNaCl})=\frac{m({\rm##sNaCl})}{M({\rm##sNaCl})}=\frac{5}{58{,}44}##s\doteq0{,}09\,\rm##smol§§
Výsledek tedy odpovídá našemu odhadu. Stejným způsobem určíme množství molů i u zbývajících prvků.
§§n({\rm##sFe})=\frac{m({\rm##sFe})}{M({\rm##sFe})}=\frac{0{,}015}{55{,}845}\doteq0{,}0003\,\rm##smol§§§§n({\rm##sK})=\frac{m({\rm##sK})}{M({\rm##sK})}=\frac{0{,}37}{39{,}098}\doteq0{,}009\,\rm##smol§§
Odpověď
Doporučená denní dávka železa činí $$0{,}0003\,\rm##smol$$, draslíku $$0{,}009\,\rm##smol$$ a soli $$0{,}09\,\rm##smol$$.

Jaká je hmotnost jednoho molu molekuly dusíku?
Řešení
| $$n(\rm##sN_2)=##s1\,##smol$$ |
| $$m(\rm##sN_2)##s=?$$ |
Ačkoli se příklad zdá velmi podobný první řešené úloze, je třeba si uvědomit rozdíl mezi atomem dusíku ($$\rm##sN$$) a molekulou dusíku ($$\rm##sN_2$$).
Z periodické tabulky prvků vyčteme molární hmotnost dusíku.
§§M({\rm##sN})=14{,}007\,##s\rm##s\frac{g}{mol}§§
Protože však zkoumáme hmotnost molekuly dusíku, určíme rovněž molární hmotnost molekuly dusíku.
§§M({\rm##sN_2})=##s2\cdot##sA{\rm_r(N)}=28{,}014\,##s\rm##s\frac{g}{mol}§§
Známé hodnoty nyní dosadíme do vzorce
§§m({\rm##sN_2})=n({\rm##sN_2})##s\cdot##sM({\rm##sN_2}).§§
Výpočet
§§m({\rm##sN_2})=n({\rm##sN_2})##s\cdot##sM({\rm##sN_2})=1##s\cdot##s28{,}014##s=##s28{,}014\,\rm##s##sg§§
Odpověď
Hmotnost jednoho molu molekuly dusíku je $$28{,}014\,\rm##sg$$.

Kolik molů uhlíku obsahuje jedna krabička Carbo medicinalis (lék na průjem známý jako černé uhlí), jestliže v ní najdeme 20 tablet a podle příbalového letáku každá obsahuje právě $$300\,\rm##smg$$ aktivního uhlí?
Řešení
| $$m(\rm##sC)=300\,\rm##smg\;\text{v##s##s1##stabletě}$$ |
| celkem 20 tablet |
I. způsob
Nejprve zjistíme, jaká je celková hmotnost uhlíku v celém balení v gramech.
Výpočet
$$m({\rm##sC})=##s20\cdot##s0{,}300##s=##s6\,\rm##sg$$
Nyní určíme molární hmotnost uhlíku a následně známé hodnoty dosadíme do vzorce pro výpočet látkového množství
§§n=\frac{m}{M}.§§
Výpočet
§§M({\rm##sC})##s=##s12{,}011\,##s\rm##s\frac{g}{mol}§§§§n({\rm##sC})=\frac{m({\rm##sC})}{M({\rm##sC})}=##s\frac{6}{12{,}011}##s\doteq##s0{,}5\,##s\rm##smol§§
Odpověď
Jedno balení aktivního uhlí Carbo medicinalis obsahuje přibližně půl molu uhlíku.
II. způsob
Další možností, jak postupovat při počítání, je využití přímé úměrnosti. První krok k zjištění celkové hmotnosti uhlíku v balení je stejný. Místo použití vzorce pro výpočet látkového množství však můžeme sestavit následující trojčlenku.
Výpočet
§§\begin{align*}##n\text{1##smol##satomů##sC}##s&##s...............##s&##s12&{,}011\,\rm##sg##s\\##nx\;\text{mol##satomů##sC}##s&##s...............##s&##s6&\,##s\rm##sg##s\\##n\hline##s\\##n\end{align*}§§
§§x=\frac{1\cdot##s6}{12{,}011}##s\doteq##s0{,}5\,\text{mol}§§
Odpověď
Jedno balení aktivního uhlí Carbo medicinalis obsahuje přibližně půl molu uhlíku.

Ze skupiny vzácných plynů je ve vzduchu nejvíce obsažen argon. Litr vzduchu obsahuje $$0{,}4##s\cdot##s10^{-3}$$ molů argonu. Jaká je hmotnost argonu v jednom litru vzduchu?
Řešení
| $$n({\rm##sAr})=0{,}4##s\cdot##s10^{-3}=0{,}000\,4\,\rm##smol$$ |
| $$m(\rm##sAr)=?$$ |
I. způsob
Než se pustíme do počítání, učiníme odhad o výsledku. Protože látkové množství argonu ve vzduchu je přibližně rovno polovině tisícíny molu, musí být i celková hmotnost přibližně rovna polovině tisíciny hmotnosti jednoho molu argonu. Jelikož molární hmotnost argonu z tabulky je rovna přibližně $$40\,\rm##sg$$, očekáváme výsledek hmotnosti argonu okolo $$0{,}02\,\rm##sg$$.
Pro výpočet tedy nejprve potřebujeme zjistit přesnou molární hmotnost argonu, tedy $$M({\rm##sAr})=39{,}948\,\rm##s\frac{g}{mol}$$. Nyní známé hodnoty látkového množství a molární hmotnosti dosadíme do vzorce
§§m=n##s\cdot##sM.§§
Výpočet
§§m({\rm##sAr})=##sn({\rm##sAr})##s\cdot##sM({\rm##sAr})=##s0{,}000\,4##s\cdot##s39{,}948##s\doteq##s0{,}016\,\rm##sg##s§§
Dostáváme tak výsledek, který odpovídá našemu dříve učiněnému odhadu.
Odpověď
Litr vzduchu obsahuje přibližně $$0{,}016\,\rm##sg##s$$ argonu.
II. způsob
Další možností, jak postupovat při výpočtu, je využití přímé úměrnosti. Místo použití vzorce pro výpočet látkového množství můžeme sestavit následující trojčlenku.
Výpočet
§§\begin{align*}##n\text{1##smol##satomů##sAr}##s&##s...............##s&##s39{,}948\,\rm##sg##s\\##n0{,}000\,4\text{##smol##satomů##sAr}##s&##s...............##s&##sx\,##s\rm##sg##s\\##n\hline##s\\##n\end{align*}§§
§§x=\frac{39{,}948\cdot##s0{,}000\,4}{1}##s\doteq##s0{,}016\,\text{g}§§
Odpověď
Litr vzduchu obsahuje přibližně $$0{,}016\,\rm##sg##s$$ argonu.

Lidské tělo syntetizuje bílkoviny z aminokyselin. Příkladem takovéto aminokyseliny je i glycin, který má molekulový vzorec $$\rm##sC_2H_5O_2N$$. Spočítejte, kolik molů molekul glycinu je obsaženo ve $$28{,}35\,\rm##sg$$ glycinu.
Řešení
| $$m(\rm##sC_2H_5O_2N)=28{,}35\,##sg$$ |
| $$n(\rm##sC_2H_5O_2N)=?$$ |
I. způsob
Protože opět máme za úkol zjistit látkové množství, potřebujeme nejprve vědět, jakou hmotnost má jeden mol glycinu. Z tabulky tedy určíme molární hmotnost.
§§\begin{align*}##nM(\rm##s{C_2H_5O_2N})##s&=##s2\cdot##sA{\rm_r}({\rm##sC})##s+##s5##s\cdot##sA{\rm_r}({\rm##sH})##s+##s2##s\cdot##sA{\rm_r}({\rm##sO})##s+##sA{\rm_r}({\rm##sN})##s\\##n##s&=##s24{,}022+5{,}040+31{,}998+14{,}007##s\\##s&\doteq##s75{,}07\,##s\rm##sg##n\end{align*}§§
Následně dopočítáme látkové množství ze vzorce
§§n=\frac{m}{M}.§§
Výpočet
§§n({\rm##sC_2H_5O_2N})=\frac{m({\rm##sC_2H_5O_2N})}{M({\rm##sC_2H_5O_2N})}=\frac{28{,}35}{75{,}07}##s\doteq##s0{,}38\,\rm##smol§§
Odpověď
Zadané množství glycinu obsahuje $$0{,}38$$ molů.
II. způsob
Další možností, jak postupovat při výpočtu, je využití přímé úměrnosti. Místo použití vzorce pro výpočet látkového množství sestavíme následující trojčlenku.
Výpočet
§§\begin{align*}##n\text{1##smol##smolekul##sglycinu}##s&##s...............##s&##s75{,}07\,\rm##sg##s\\##nx\;\text{mol##smolekul##s##sglycinu}##s&##s...............##s&##s28{,}35\,\rm##sg##s\\##n\hline##s\\##n\end{align*}§§
§§x=\frac{1\cdot##s28{,}35}{75{,}07}##s\doteq##s0{,}38##s\,\text{mol}§§
Odpověď
Zadané množství glycinu obsahuje $$0{,}38$$ molů.

Bez použití tabulky periodické soustavy prvků spočítejte molární hmotnost uhličitanu vápenatého, pokud víte, že $$5$$ molů této látky váží $$500{,}45\,\rm##sg$$.
Řešení
| $$n(\rm##sCaCO_3)=5\,mol$$ |
| $$m(\rm##sCaCO_3)=500{,}45\,##sg$$ |
| $$M(\rm##sCaCO_3)=?$$ |
I. způsob
Můžeme vyjít ze znalosti přímé úměry a sestavit následující trojčlenku.
Výpočet
§§\begin{align*}##n\text{5##smolů}\;\rm##sCaCO_3##s&##s...............##s&##s500{,}45\,##s\rm##sg##s\\##n\text{1##smol}\;\rm##sCaCO_3##s&##s...............##s&##sx\,##s\rm##sg##s\\##n\hline##s\\##n\end{align*}§§
§§x=\frac{500{,}45\cdot##s1}{5}##s\doteq##s100{,}09\,\text{g}§§
Dostáváme tak výsledek, který odpovídá hodnotě vypočtené pomocí tabulek.
Odpověď
Molární hmotnost uhličitanu vápenatého je $$100{,}09\,\rm##s\frac{g}{mol}.$$
II. způsob
Další možností, jak postupovat při výpočtu, je využití vzorce
§§##sM=\frac{m}{n}.§§
Následně dosadíme známé hodnoty hmotnosti a látkového množství.
Výpočet
$$M=\frac{m}{n}=\frac{500{,}45}{5}=100{,}09\,##s\rm##sg$$
Odpověď
Molární hmotnost uhličitanu vápenatého je $$100{,}09\,\rm##s\frac{g}{mol}.$$

Vitamín C je kovalentní sloučenina s molekulovým vzorcem $$\rm##sC_6H_8O_6$$. Doporučená denní dávka (DDD) vitamínu C pro děti v rozmezí 4–8 let je $$1{,}42##s\cdot##s10^{-4}\,\rm##smol$$. Kolik gramů vitamínu C by měly děti denně podle tabulek DDD přijímat v potravě?
Řešení
| $$n(\rm##sC_6H_8O_6)=1{,}42\cdot##s10^{-4}\,mol$$ |
| $$m(\rm##sC_6H_8O_6)=?$$ |
Nejprve s pomocí periodické tabulky určíme molární hmotnost vitamínu C.
$$M({\rm##sC_6H_8O_6})=6##s\cdot##s12{,}011+##s8\cdot##s1{,}008##s+6\cdot##s15{,}999##s\doteq##s176{,}12\,\rm##s##s\frac{g}{mol}.$$
Než začneme s výpočtem, zamyslíme se nad očekávanou hodnotou výsledku. Jelikož zadané množství molů je velmi malé (zhruba jedna desetitisícina molu), bude i výsledná hmotnost velmi malá, a to přibližně jedna desetitisícina určené molární hmotnosti, což je zaokrouhleně $$0{,}02\,\rm##sg$$.
I. způsob
Nyní můžeme úvahou pomocí přímé úměry sestavit trojčlenku a dopočítat požadovanou hmotnost vitamínu C.
Výpočet
§§\begin{align*}##n\text{1##smol}\;\rm##sC_6H_8O_6##s##s&##s...............##s&##s176{,}12\,##s\rm##sg##s\\##n1{,}42##s\cdot##s10^{-4}\text{##smolů}\;\rm##sC_6H_8O_6##s&##s...............##s&##sx\,##s\rm##sg##s\\##n##n\hline##s\\##n\end{align*}§§
§§x=\frac{176{,}12\cdot##s1{,}42##s\cdot##s10^{-4}}{1}##s\doteq##s0{,}025\,\text{g}§§
Vypočítaná hmotnost odpovídá našemu předem učiněnému odhadu.
Odpověď
Doporučená denní dávka vitamínu C pro děti ve věku od 4 do 8 let činí $$0{,}025\,##s\rm##sg$$.
II. způsob
Další možností, jak postupovat při výpočtu, je využití známého vzorce $$n=##s\frac{m}{M}$$, odkud vyjádříme hmotnost látky jako:
§§m=##sn##s\cdot##sM.§§
Následně dosadíme známé hodnoty molární hmotnosti a látkového množství.
Výpočet
$$m= ##sn##s\cdot##sM##s=##s1{,}42\cdot##s10^{-4}##s\cdot##s176{,}12\doteq##s0{,}025\,##s\rm##sg$$
Odpověď
Doporučená denní dávka vitamínu C pro děti ve věku od 4 do 8 let činí $$0{,}025\,##s\rm##sg.$$

Jaká je hmotnost $$0{,}443$$ molu hydrazinu $$\rm##sN_2H_4$$?
Řešení
| $$n({\rm##sN_2H_4})=0{,}443\,\rm##smol$$ |
| $$m(\rm##sN_2H_4)=?$$ |
Nejprve s pomocí periodické tabulky určíme molární hmotnost hydrazinu.
$$M(\rm##sN_2H_4)=##s2\cdot##s14{,}007+##s4\cdot##s1{,}008\doteq##s32{,}05\,##s\frac{g}{mol}.$$
Opět zkusíme učinit odhad o výsledku. Jelikož zadané látkové množství je přibližně rovno $$\frac{2}{5}$$, očekáváme výsledek roven asi $$\frac{2}{5}$$ molární hmotnosti hydrazinu, tedy hmotnost okolo $$13\,\rm##sg$$.
I. způsob
Nyní můžeme úvahou pomocí přímé úměry sestavit trojčlenku a dopočítat požadovanou hmotnost hydrazinu.
Výpočet
§§\begin{align*}##n\text{1##smol}\;\rm##sN_2H_4##s##s&##s...............##s&##s32{,}05\,##s\rm##sg##s\\##n0{,}443##s\text{##smol}\;\rm##sN_2H_4##s&##s...............##s&##sx\,##s\rm##sg##s\\##n##n\hline##s\\##n\end{align*}§§
§§x=\frac{32{,}05\cdot##s0{,}443}{1}##s\doteq##s14{,}2\,\text{g}§§
Vypočítaná hmotnost odpovídá našemu předem učiněnému odhadu.
Odpověď
Hmotnost $$0{,}443$$ molů hydrazinu je $$14{,}2\,\rm##sg$$.
II. způsob
Další možností, jak postupovat při výpočtu, je využití známého vzorečku $$n=##s\frac{m}{M}$$, odkud vyjádříme hmotnost látky jako:
§§m= ##sM##s\cdot##sn.§§
Následně dosadíme známé hodnoty molární hmotnosti a látkového množství.
Výpočet
§§m= ##sM##s\cdot##sn##s=##s32{,}05##s\cdot##s0{,}443##s\doteq##s14{,}2\,\rm##sg§§
Odpověď
Hmotnost $$0{,}443$$ molů hydrazinu je $$14{,}2\,\rm##sg$$.

Měď je pro svoji výbornou elektrickou vodivost hojně využívána k výrobě elektrických vodičů, elektromotorů či elektrických obvodů. Kolik atomů mědi je přítomno ve $$5{,}00\,\rm##sg$$ měděného drátku?
Řešení
| $$m(\rm##sCu)=5\,\rm##sg$$ |
| $$N(\rm##sCu)=?$$ |
Nejprve s pomocí periodické tabulky určíme molární hmotnost mědi.
§§\rm##sM(Cu)=##s63{,}546\,##s\frac{g}{mol}.§§
I v tomto případě se můžeme pokusit učinit odhad o výsledku. Je to vhodné zejména proto, že představit si atomy a jejich počet je velmi složité. Protože zadané množství 5 gramů mědi je méně než $$\frac{1}{10}$$ molární hmotnosti mědi ($$\sim##s64\,\rm##sg$$, tj. hmotnost 1 molu mědi), musí být výsledný počet atomů rovněž menší než $$\frac{1}{10}$$ počtu atomů v jednom molu (Avogradrova konstanta $$N{\rm##s_A}=6{,}022##s\cdot##s10^{23}\,\rm##smol^{-1}$$), tedy řádově očekáváme $$10^{22}$$ atomů mědi.
I. způsob
Využijeme znalost definice molu. Víme, že v jednom molu jakékoli látky se nachází právě $$6{,}022##s\cdot##s10^{23}$$ částic. Proto potřebujeme zjistit, kolika molům odpovídá zadané množství mědi. Látkové množství mědi určíme buď ze vzorce $$n=##s\frac{m}{M}$$, nebo pomocí trojčlenky jako v předchozích řešených příkladech.
§§n=##s\frac{5}{63{,}546}##s\doteq##s0{,}079\,\rm##smol§§
Nyní úvahou o přímé úměrnosti můžeme sestavit následující trojčlenku.
Výpočet
§§\begin{align*}##n\text{1##smol}\;\rm##sCu##s##s&##s...............##s&##s6{,}022##s\cdot##s10^{23}\,##s\text{atomů}##s\\##n0{,}079##s\text{##smol}\;\rm##sCu##s&##s...............##s&##sx\,\text{atomů}##s\\##n##n\hline##s\\##n\end{align*}§§
§§x=\frac{6{,}022##s\cdot##s10^{23}\cdot##s0{,}079}{1}##s\doteq##s4{,}76##s\cdot##s10^{22}\,\text{atomů}§§
Odpověď
Pět gramů měděného drátku obsahuje $$4{,}76##s\cdot##s10^{22}$$ atomů mědi.
II. způsob
Další možností, jak postupovat při výpočtu, je využití známého vzorečku $$n=##s\frac{N}{N{\rm##s_A}}$$, odkud vyjádříme počet atomů mědi jako:
§§##sN=##sn##s\cdot##sN{\rm##s_A}§§
Ze vzorce $$n=\frac{m}{M}$$ či pomocí trojčlenky určíme jako v předchozích příkladech látkové množství zadaného množství mědi. Tedy určíme molární hmotnost z tabulky $$M(\rm##sCu)=##s63{,}546\,##s\rm\frac{g}{mol}$$ a vypočteme látkové množství$$n=##s\frac{5}{63{,}546}##s\doteq##s0{,}079\,\rm##smol$$
Následně dosadíme známé hodnoty látkového množství a Avogadrovy konstanty do vzorce pro výpočet počtu částic.
Výpočet
§§N=##sn##s\cdot##sN{\rm_A}##s=0{,}079##s\cdot ##s6{,}022##s\cdot##s10^{23}##s\doteq##s4{,}76##s\cdot##s10^{22}\,\text{částic}§§
Odpověď
Pět gramů měděného drátku obsahuje $$4{,}76##s\cdot##s10^{22}$$ atomů mědi.
III. způsob
Po vzoru prvního řešení využijeme úvahy a zkombinujeme dvě přímé úměry. Využijeme znalosti látkového množství mědi a počtu atomů mědi v jednom molu látky.
Výpočet
§§\begin{align*}##n\text{1##smol}\;\rm##sCu##s##s&##s...............##s&##s63{,}546\,##s\rm##sg##s\;Cu##s&...............##s##s&##s6{,}022##s\cdot##s10^{23}\,##s\text{atomů##sCu}##s\\##nx\;##s\text{mol}\;\rm##sCu##s&##s...............##s&##s5\rm##s\,g##s\;##sCu##s&...............##s&##sy\,\text{atomů##sCu}##s\\##n##n\hline##s\\##n\end{align*}##n##n§§
§§x=\frac{6{,}022##s\cdot##s10^{23}\cdot##s5}{63{,}546}##s\doteq##s4{,}74##s\cdot##s10^{22}\,\text{atomů}§§
Odpověď
Pět gramů měděného drátku obsahuje $$4{,}74##s\cdot##s10^{22}$$ atomů mědi.
Poznámka
Výsledky se liší vlivem případného zaokrouhlení mezivýpočtu látkového množství.

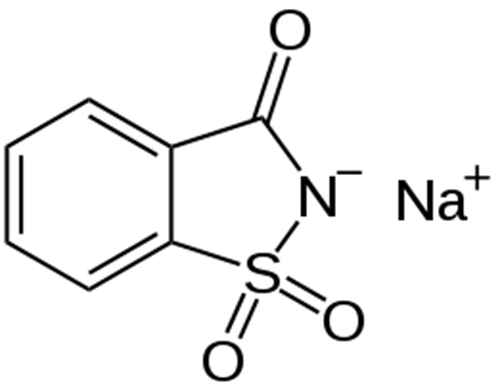
Sacharin je nejstarším umělým sladidlem. Byl objeven už v roce 1879 a to náhodou, když si profesor Ira Ramsen po práci s deriváty uhelného dehtu špatně umyl ruce a při večeři ucítil nečekanou sladkost. V porovnání se sacharosou je asi třistakrát sladší, nicméně po něm v ústech zůstává kovová pachuť, a to především ve větších koncentracích. Balení $$50\,\rm##sg$$ umělého sladidla na bázi sacharinu ve svém složení deklaruje množství $$27\,\%$$ sacharinu sodného ($$\rm##sC_7H_4NNaO_3S$$) jako sladicí složky. Molární hmotnost sacharinu sodného byla stanovena na $$241{,}19\,\rm##s\frac{g}{mol}$$.
1. Kolik molekul sacharinu sodného je přítomno v jednom balení?
2. Určete i počet atomů uhlíku obsaženého v 1 balení sladidla.
3. Nakonec spočítejte, kolik molekul sacharinu sodného je v jedné tabletě, jestliže balení obsahuje 800 tablet.
Řešení
| Hmotnost balení: $$50\,\rm##sg$$ z toho $$27\,\%$$ sacharinu sodného |
| $$M(\rm##sC_7H_4NNaO_3S)=241{,}19\,\frac{g}{mol}$$ |
I. otázka
Nejprve ze znalosti celkové hmotnosti balení a procentuálního zastoupení sladící složky vypočteme hmotnost sacharinu sodného.
$$m(##s\rm##sC_7H_4NNaO_3S)=##s50##s\cdot##s0{,}27##s=##s13{,}5\,##sg$$
Z vypočtené skutečné hmotnosti sacharinu sodného určíme jeho látkové množství ze vzorce $$n=\frac{m}{M}.$$
§§n(##s\rm##sC_7H_4NNaO_3S)=##s\frac{13{,}5}{241{,}19}##s\doteq##s0{,}056\,##smol§§
Nyní konečně můžeme přistoupit k určení počtu molekul sacharinu sodného. Stejně jako v předchozích řešených příkladech je možno úlohu vyřešit pomocí trojčlenky na přímou úměru či pomocí vzorce $$n=\frac{N}{N{\rm##s_A}}$$. V našem případě sestavíme trojčlenku.
Výpočet
§§\begin{align*}##n\text{1##smol##ssacharinu##ssodného}##s&##s...............##s&##s6{,}022##s\cdot##s10^{23}\,\text{částic}##s\\##n0{,}056\text{##smol##ssacharinu##ssodného}##s&##s...............##s&##sx\,##s\text{částic}##s\\##n\hline##s\\##n\end{align*}§§
§§x=\frac{6{,}022##s\cdot##s10^{23}\cdot##s0{,}056}{1}##s\doteq##s3{,}37##s\cdot##s10^{22}##s\,\text{částic}§§
Odpověď
Balení obsahuje $$3{,}37##s\cdot##s10^{22}$$ molekul sacharinu sodného.
II. otázka
Nyní zjistíme celkový počet atomů uhlíku v jednom balení sacharinu. Ze sumárního vzorce $$\rm##sC_7H_4NNaO_3S$$ vidíme, že jedna molekula sacharinu sodného obsahuje právě 7 atomů uhlíku. Úvahou tedy sestavíme následující trojčlenku na přímou úměrnost.
Výpočet
§§\begin{align*}##n\text{1##smolekula##ssacharinu##ssodného}##s&##s...............##s&##s7##s\;\text{atomů##suhlíku}\\##n3{,}37##s\cdot##s10^{22}\text{##smolekul##ssacharinu##ssodného}##s&##s...............##s&##sx\;\text{atomů##suhlíku}##s\\##n\hline##s\\##n\end{align*}§§
§§x=\frac{7\cdot##s3{,}37##s\cdot##s10^{22}}{1}##s\doteq##s2{,}36##s\cdot##s10^{23}\;\text{atomů##suhlíku}§§
Odpověď
V molekulách sacharinu sodného je přítomno $$2{,}36##s\cdot##s10^{23}$$ atomů uhlíku.
III. otázka
Pro určení počtu molekul sacharinu v jedné tabletě vyjdeme z úvahy, že celé balení umělého sladidla obsahuje 800 tablet. V první otázce jsme navíc určili celkové množství molekul sacharinu sodného v balení, a to $$3{,}37##s\cdot##s10^{22}$$ molekul. Pak jedna tableta obsahuje právě
§§N_{\text{1##stableta}}=##s\frac{3{,}37##s\cdot##s10^{22}}{800}=4{,}21##s\cdot##s10^{19}\;\text{molekul##ssacharinu##ssodného.}§§
Odpověď
Jedna tableta umělého sladidla obsahuje $$4{,}21##s\cdot##s10^{19}$$ molekul sacharinu sodného.

Jaká je hmotnost $$10^{23}$$ atomů zlata?
Řešení
| $$N(\rm##sAu)=10^{23}\,\text{atomů}$$ |
| $$m(\rm##sAu)=?\,g$$ |
Následující úlohu je možné řešit i čtyřmi různými způsoby. Pro každý z nich budeme potřebovat hodnotu molární hmotnosti zlata, kterou vyčteme z tabulek, protože je číselně rovna relativní atomové hmotnosti.
§§M(\rm##sAu)=196{,}97\,\frac{g}{mol}§§
I. způsob
Úlohu vyřešíme úvahou s použitím přímé úměrnosti. Ze znalosti počtu částic v jednom molu látky můžeme určit, jaké látkové množství odpovídá zadanému počtu atomů zlata. Sestavíme proto následující trojčlenku.
Výpočet
§§\begin{align*}##n\text{1##smol}\;\rm##sAu##s##s&##s...............##s&##s6{,}022##s\cdot##s10^{23}\,##s\text{atomů##szlata}##s\\##n##s\text{##sx##smol}\;\rm##sAu##s&##s...............##s&##s10^{23}\,\text{atomů##szlata}##s\\##n##n\hline##s\\##n\end{align*}§§
§§x=\frac{1\cdot##s10^{23}}{6{,}022##s\cdot##s10^{23}}##s\doteq##s0{,}166\,\text{mol}§§
Vypočtené získané látkové množství zlata nyní použijeme k výpočtu hmotnosti, a to opět s využitím přímé úměry.
§§\begin{align*}##n\text{1##smol}\;\rm##sAu##s##s&##s...............##s&##s196{,}97\,##s\text{g}##s\\##n##s0{,}166\;\text{mol}\;\rm##sAu##s&##s...............##s&##sx\,\text{g}##s\\##n##n\hline##s\\##n\end{align*}§§
§§x=\frac{196{,}97##s\cdot##s0{,}166}{1}##s\doteq##s32{,}70\,\text{g}§§
Odpověď
Zadané množství $$10^{23}$$ atomů zlata váží $$32{,}70\,\rm##sg$$.
II. způsob
Nyní vyřešíme úlohu úvahou s kombinací dvou přímých úměr zároveň. Ze známých hodnot Avogadrovy konstanty a molární hmotnosti zlata a počtu částic zlata sestavíme následující schéma využívající dvě přímé úměry.
Výpočet
§§\begin{align*}##n\text{1##smol}\;\rm##sAu##s##s&##s...............##s&##s6{,}022##s\cdot##s10^{23}\,##s\text{atomů##sAu}##s&##s...............##s&##s##s196{,}97\,##s\text{g##sAu}\\##n\text{x##smol}\;\rm##sAu##s&##s...............##s&##s10^{23}\,\text{atomů##sAu}##s&##s...............##s&##sy\,##s\text{g##sAu}\\##n##n\hline##s\\##n\end{align*}§§
Protože potřebujeme znát pouze neznámou $$y$$, nebudeme počítat neznámou $$x$$.
§§y=\frac{196{,}97\cdot##s10^{23}}{6{,}022##s\cdot##s10^{23}}##s\doteq##s32{,}71##s\,\text{g}§§
Odpověď
Zadané množství $$10^{23}$$ atomů zlata váží $$32{,}71\,\rm##sg$$.
III. způsob
Pokud ale nechceme úlohu řešit pomocí úvahy, můžeme postupně dosazovat do jednotlivých vztahů pro látkové množství.
Výpočet
Nejprve tedy ze vzorce $$n=\frac{N}{N{\rm##s_A}}$$ určíme látkové množství zadaných atomů zlata.
§§n(\rm##sAu)=\frac{10^{23}}{6{,}022##s\cdot##s10^{23}}##s\doteq##s0{,}166\,\text{mol}§§
Nyní spočtené látkové množství dosadíme do vzorce $$n=\frac{m}{M}$$, odkud si vyjádříme skutečnou hmotnost zlata.
$$m({\rm##sAu})=##sn##s\cdot##sM##s=##s0{,}166##s\cdot##s196{,}97##s\doteq##s32{,}70\,\text{g}$$
Odpověď
Zadané množství $$10^{23}$$ atomů zlata váží $$32{,}70\,\rm##sg$$.
IV. způsob
Poslední způsob je elegantnější variantou III. možnosti. Opět využijeme vzorce pro látkové množství, avšak místo postupného počítání jednotlivých veličin nejprve zkombinujeme potřebné vzorce pro výpočet skutečné hmotnosti a konkrétní hodnoty dosadíme až na konec.
Výpočet
K určení skutečné hmotnosti zadaného počtu atomů zlata je třeba znát látkové množství, které určíme ze vzorce $$n=\frac{N}{N{\rm##s_A}}$$. Dále využijeme odvozený vztah pro výpočet hmotnosti $$##sm=##sn##s\cdot##sM$$, kam dosadíme vyjádření pro látkové množství. Získáme následující vztah pro výpočet, do kterého dosadíme známé hodnoty.
$$m({\rm##sAu})=\frac{N}{N{\rm_A}}##s\cdot##sM##s=##s\frac{10^{23}}{6{,}022##s\cdot##s10^{23}}##s\cdot##s196{,}97##s\doteq##s32{,}71\,\text{g}.$$
Odpověď
Zadané množství $$10^{23}$$ atomů zlata váží $$32{,}71\,\rm##sg$$.

Jaká je hmotnost $$6{,}022##s\cdot##s10^{21}$$ molekul oxidu siřičitého?
Řešení
| $$N(\rm##sSO_2)=6{,}022##s\cdot##s10^{21}\,\text{molekul}$$ |
| $$m(\rm##sSO_2)=?\,g$$ |
Následující úlohu je opět možné řešit až čtyřmi různými způsoby, po vzoru předchozího řešeného příkladu. Ještě jednou projedeme všechny možné postupy vedoucí k výsledku, tentokrát již ale s kratším komentářem.
Nejprve stanovíme molární hmotnost oxidu siřičitého.
§§M(\rm##sSO_2)=64{,}06\,\frac{g}{mol}§§
Vzhledem k zadané hodnotě počtu molekul oxidu siřičitého velmi jednoduše učiníme odhad o výsledku. Jelikož počet molekul oxidu je právě stokrát menší, než je počet částic v jednom molu (Avogadrova konstanta $$6{,}022##s\cdot##s10^{23}\,\rm##smol^{-1}$$), pak i výsledná hmotnost musí být stokrát menší než je molární hmotnost oxidu, čili přibližně přesně $$0{,}64\,\rm##sg$$.
I. způsob
Úlohu vyřešíme úvahou s použitím přímé úměrnosti. Sestavíme proto následující trojčlenku.
Výpočet
§§\begin{align*}##n\text{1##smol}\;\rm##sSO_2##s##s&##s...............##s&##s6{,}022##s\cdot##s10^{23}\,##s\text{molekul}\;\rm##sSO_2##s\\##n##sx\;\text{mol}\;\rm##sSO_2##s&##s...............##s&##s6{,}022##s\cdot##s10^{21}\,\text{molekul}\;##s\rm##sSO_2##s\\##n##n\hline##s\\##n\end{align*}§§
§§x=\frac{1\cdot##s6{,}022##s\cdot##s10^{21}}{6{,}022##s\cdot##s10^{23}}##s\doteq##s0{,}01\,\text{mol}§§
Vypočtené získané látkové množství oxidu nyní použijeme k výpočtu hmotnosti, a to opět s využitím přímé úměry.
§§\begin{align*}##n\text{1##smol}\;\rm##sSO_2##s##s&##s...............##s&##s64{,}06\,\text{g}##s\\##n##s0{,}01\;\text{mol}\;\rm##sSO_2##s&##s...............##s&##sx\,\text{g}##s\\##n##n\hline##s\\##n\end{align*}§§
§§x=\frac{64{,}06##s\cdot##s0{,}01}{1}##s\doteq##s0{,}64\,\text{g}§§
Dostali jsme výsledek odpovídající našemu odhadu.
Odpověď
Zadané množství $$6{,}022##s\cdot##s10^{21}$$ molekul oxidu siřičitého váží $$0{,}64\,\rm##sg$$.
II. způsob
Nyní vyřešíme úlohu úvahou s kombinací dvou přímých úměr zároveň.
Výpočet
§§\begin{align*}##n\text{1##smol}\;\rm##sSO_2##s##s&##s...............##s&##s6{,}022##s\cdot##s10^{23}\,##s\text{molekul}\;\rm##sSO_2##s&##s...............##s&##s##s64{,}06\,##s\text{g}\;\rm##sSO_2\\##nx\;\text{mol}\;\rm##sSO_2&##s...............##s&##s6{,}022##s\cdot##s10^{21}\,\text{molekul}\;\rm##sSO_2##s&##s...............##s&##sy\,##s\text{g}\;\rm##sSO_2\\##n##n\hline##s\\##n\end{align*}§§
Odtud vypočteme hledanou neznámou $$y$$.
§§y=\frac{64{,}06\cdot##s6{,}022##s\cdot##s10^{21}}{6{,}022##s\cdot##s10^{23}}##s\doteq##s0{,}64##s\,\text{g}§§
Odpověď
Zadané množství $$6{,}022##s\cdot##s10^{21}$$ molekul oxidu siřičitého váží $$0{,}64\,\rm##sg$$.
III. způsob
Nyní budeme postupovat s použitím vzorců pro látkové množství s postupným výpočtem a dosazením.
Výpočet
Nejprve tedy ze vzorce $$n=\frac{N}{N{\rm##s_A}}$$ určíme látkové množství zadaných molekul oxidu.
§§n(\rm##sSO_2)=\frac{6{,}022##s\cdot##s10^{21}}{6{,}022##s\cdot##s10^{23}}##s\doteq##s0{,}01\,\text{mol}§§
Nyní spočtené látkové množství dosadíme do vzorce $$n=\frac{m}{M}$$, odkud si vyjádříme skutečnou hmotnost oxidu.
§§m({\rm##sSO_2})=##sn##s\cdot##sM##s=##s0{,}01##s\cdot##s64{,}06##s\doteq##s0{,}64\,\text{g}§§
Odpověď
Zadané množství $$6{,}022##s\cdot##s10^{21}$$ molekul oxidu siřičitého váží $$0{,}64\,\rm##sg$$.
IV. způsob
Nakonec užijeme odvození obecného vztahu pro výpočet hmotnosti ze vzorečků pro látkové množství.
Výpočet
K určení skutečné hmotnosti je třeba znát látkové množství, které určíme ze vzorce $$n=\frac{N}{N{\rm##s_A}}$$. Dále využijeme odvozený vztah pro výpočet hmotnosti $$m=##sn##s\cdot##sM$$, kam dosadíme vyjádření pro látkové množství. Získáme následující vztah pro výpočet, do kterého dosadíme známé hodnoty.
§§m({\rm##sSO_2})=\frac{N}{N_A}##s\cdot##sM##s=##s\frac{6{,}022##s\cdot##s10^{21}}{6{,}022##s\cdot##s10^{23}}##s\cdot##s64{,}06##s\doteq##s0{,}64\,\text{g}§§
Odpověď
Zadané množství $$6{,}022##s\cdot##s10^{21}$$ molekul oxidu siřičitého váží $$0{,}64\,\rm##sg$$.

Balení Dr. Oetker Jedlá soda obsahuje právě $$15\,##s\rm##sg$$ hydrogenuhličitanu sodného. Kolik molekul jedlé sody je v balíčku?
Řešení
| $$m(\rm##sNaHCO_3)=15\,\rm##sg$$ |
| $$N(\rm##sNaHCO_3)=\,?\,\text{molekul}$$ |
Následující úlohu je opět možné řešit až čtyřmi různými způsoby. Opět ukážeme všechny čtyři s kratším komentářem.
Nejprve stanovíme molární hmotnost hydrogenuhličitanu sodného.
§§M(\rm##sNaHCO_3)=##s84{,}01\,\frac{g}{mol}§§
Zkusme nejprve odhadnout výsledek. Molární hmotnost jedlé sody je přibližně 6krát větší než je hmotnost balení ($$15\,##s\rm##sg$$). Jeden mol (tedy $$84{,}01\,\rm##sg$$) obsahuje právě $$6{,}022##s\cdot##s10^{23}$$ molekul jedlé sody (Avogadrova konstanta). Pak šestinové množství molu ($$15\,##s\rm##sg$$) musí obsahovat i šestinové množství molekul, tedy rozměrově očekáváme výsledek $$1##s\cdot##s10^{23}$$ molekul.
I. způsob
Úlohu vyřešíme úvahou s použitím přímé úměrnosti. Sestavíme proto následující trojčlenku. Využijeme znalosti počtu molekul v jednom molu látky. Tedy jeden mol jedlé sody má hmotnost $$84{,}01\,\rm##sg$$ a obsahuje právě $$6{,}022##s\cdot##s10^{23}$$ částic.
Výpočet
§§\begin{align*}##n84{,}01\,\text{g}\;\rm##sNaHCO_3##s##s&##s...............##s&##s6{,}022##s\cdot##s10^{23}\,##s\text{molekul}\;\rm##sNaHCO_3##s\\##n##s15\,\text{g}\;{\rm##sNaHCO_3}##s&##s...............##s&##s##sx\,\text{molekul}\;\rm##sNaHCO_3##s\\##n##n\hline##s\\##n\end{align*}§§
§§x=\frac{##s6{,}022##s\cdot##s10^{23}\cdot##s15}{84{,}01}##s\doteq##s1{,}08##s\cdot##s10^{23}\,\text{molekul}§§
Výsledek odpovídá našemu dopředu učiněnému odhadu.
Odpověď
Balíček jedlé sody obsahuje $$1{,}08##s\cdot##s10^{23}$$ molekul hydrogenuhličitanu sodného.
II. způsob
Nyní vyřešíme úlohu úvahou s kombinací dvou přímých úměr zároveň.
Výpočet
§§\begin{align*}##n\text{1##smol}\;\rm##sNaHCO_3##s##s&##s...............##s&##s6{,}022##s\cdot##s10^{23}\,##s\text{molekul}\;\rm##sNaHCO_3##s&##s...............##s&##s##s84{,}01\,##s\text{g}\;\rm##sNaHCO_3\\##nx\;\text{mol}\;\rm##sNaHCO_3&##s...............##s&##sy##s\,\text{molekul}\;\rm##sNaHCO_3##s&##s...............##s&##s15\,##s\text{g}\;\rm##sNaHCO_3\\##n##n\hline##s\\##n\end{align*}§§
Odtud vypočteme hledanou neznámou $$y$$.
§§y=\frac{##s6{,}022##s\cdot##s10^{23}\cdot##s15}{84{,}01}##s\doteq##s1{,}08##s\cdot##s10^{23}##s\,\text{molekul}§§
Odpověď
Balíček jedlé sody obsahuje $$1{,}08##s\cdot##s10^{23}$$ molekul hydrogenuhličitanu sodného.
III. způsob
Nyní budeme postupovat s použitím vzorců pro látkové množství s postupným výpočtem a dosazením.
Výpočet
Nejprve tedy ze vzorce $$n=\frac{m}{M}$$ určíme látkové množství jedlé sody v balení.
§§n({\rm##sNaHCO_3})=\frac{m}{M}##s=##s\frac{15}{84{,}01}##s\doteq##s0{,}179##s\,\text{mol}§§
Nyní spočtené látkové množství dosadíme do vzorce $$n=\frac{N}{N{\rm_A}}$$, odkud si vyjádříme množství částic $$N$$.
§§N({\rm##sNaHCO_3})=##sn##s\cdot##sN{\rm##s_A}##s=##s0{,}179##s\cdot##s6{,}022##s\cdot##s10^{23}##s\doteq##s1{,}08##s\cdot##s10^{23}\,\text{molekul}§§
Odpověď
Balíček jedlé sody obsahuje $$1{,}08##s\cdot##s10^{23}$$ molekul hydrogenuhličitanu sodného.
IV. způsob
Nakonec užijeme odvození obecného vztahu pro výpočet hmotnosti ze vzorců pro látkové množství.
Výpočet
K určení skutečné hmotnosti je třeba znát látkové množství, které určíme ze vzorce $$n=\frac{m}{M}$$. Dále využijeme odvozený vztah pro výpočet počtu částic $$##sN=##sn##s\cdot##sN{\rm_A}$$, kam dosadíme vyjádření pro látkové množství. Získáme následující vztah pro výpočet, do kterého dosadíme známé hodnoty.
§§N({\rm##sNaHCO_3})=\frac{m}{M}##s\cdot##sN{\rm_A}=##s\frac{15}{84{,}01}##s\cdot##s6{,}022##s\cdot##s10^{23}##s\doteq##s1{,}08##s\cdot##s10^{23}\,\text{molekul}§§
Odpověď
Balíček jedlé sody obsahuje $$1{,}08##s\cdot##s10^{23}$$ molekul hydrogenuhličitanu sodného.
Videa s danou problematikou
Khan Academy: Řešené příklady na výpočet látkového množství
Jaroslav Peřka: Molární hmotnost
Isibalo: Látkové množství
Isibalo: Bilance látkových množství

Dalším umělým hojně využívaným sladidlem je aspartam (E951). To proto, že nemá takovou kovovou pachuť jako sladidla na bázi sacharinu. V porovnání se sacharosou je asi 150x sladší. Nicméně zahříváním se rozkládá, čímž ztrácí svoji sladkou chuť, a tak se místo k pečení využívá spíše ke slazení nápojů, které deklarují obsah $$0\,\%$$ cukru. Při pití „dietních“ limonád však mějme na paměti, že látka byla označena za rakovinotvornou a navíc zvyšuje riziko poškození mozku. Konzumace aspartamu (a i dalších umělých sladidel) by tedy měla být minimální, ne-li zcela omezená.